الأنيق...}
مستشار اداري


 عدد الرسائل : 216 عدد الرسائل : 216
العمر : 37
رقم العضوية : 700
تاريخ التسجيل : 26/10/2008
 |  موضوع: بــحــوث الـعـمـلـيـات موضوع: بــحــوث الـعـمـلـيـات 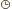 الأحد مارس 15, 2009 11:20 am الأحد مارس 15, 2009 11:20 am | |
| [size=18] I – 1 تعريف بحوث العمليات
إن عملية اتخاذ القرارات هي عملية ملازمة للإنسان منذ أول نشأته، حيث كان عليه أن يقرر كيف يعيش وأين يعيش، وكيف يحمي نفسه. كما أنه كان بحاجة إلى اتخاذ قرار بشأن أية مشكلة تواجهه في حياته. لقد كان الأفراد يتخذون قراراتهم معتمدين على قدراتهم و خبراتهم و ظروفهم الشخصية، و البيئة التي يعيشون فيها والتي تشكل بحد ذاتها تعقيداً لهذه العملية إضافة إلى الصعوبة المتمثلة بعدم توافر أسس علمية ثابتة و متعارف عليها لهذه العملية. إلا أنه و نتيجة لازدياد حجم المشاكل التي تواجه الإنسان وتداخلها وتقسيم العمل وتعدد الإدارات والأقسام، وكذلك تنوع المنتجات والسلع الذي أدى إلى تعقيد الأعمال وظهور كثير من المشكلات الإدارية والإنتاجية، كان لا بد من البحث عن أساليب أكثر ملاءمة وفعالية لمواجهة هذه المشكلات.
نطلق على مجموعة الأساليب العلمية المستخدمة في تحليل المشكلات والبحث عن الحلول المثلى اسم بحوث العمليات، أو بتعبير آخر، بحوث العمليات هي مصطلح أطلق على مجموعة البحوث والدراسات التي تساعدنا على اتخاذ قرار علمي ومدروس للقيام بعمل ما على أفضل وجه وضمن الإمكانات المتاحة.
تعد بحوث العمليات من العلوم التطبيقية الحديثة التي أحرزت تطبيقاتها نجاحاً واسعاً في مختلف مجالات الحياة. إن الخاصية التي يتميز بها هذا العلم هو إعداد نموذج علمي و عملي لنظام معين يتضمن تحديد العوامل المؤثرة و التنبؤ و مقارنة النتائج لمساعدة الادارة في قياس دقة النظام المستخدم و من ثم إتخاذ القرارت المناسبة و السليمة. نلاحظ مما سبق أن تعريف بحوث العمليات يركز على النواحي الأساسية الآتية:
• أن بحوث العمليات تستخدم الطريقة العلمية كأساس و منهج في البحث والدراسة.
• أن جوهر بحوث العمليات هو بناء نموذج و الاعتماد عليه.
• إن الهدف من بحوث العمليات هو مساعدة الإدارة في اتخاذ القرارات المتعلقة بالمشكلات الإدارية الصعبة و المعقدة.
I – 2 تاريخ بحوث العمليات
بما أنه يصعب تحديد فترة معينة بوصفها نقطة بداية لتطبيق مفاهيم بحوث العمليات، إلا أنه و من خلال استعراض تطور مفهوم الإدارة بشكلٍ عام، نستطيع أن نرى أن هناك فترات بدأت تتميز بها هذه المفاهيم أكثر من غيرها كفترة الثورة الصناعية مثلاً. وبالرغم من ذلك فإنه يمكن القول إن بحوث العمليات لم تظهر حقلاً علمياً مستقلاً إلا في بداية الحرب العالمية الثانية. حيث شكَّلَت بريطانيا فريقاً من العلماء يشمل مختلف المجالات العلمية للبحث عن أفضل الأساليب والوسائل العلمية لاستخدامها في طريقة توزيعٍ أفضل للقوات العسكرية، وكذلك في استخدام الأجهزة المتطورة كقاذفات القنابل والرادارات لكسب الحرب. كما شكَّلَت الولايات المتحدة الأمريكية فريقاً آخر من العلماء في تخصصات مختلفة لمعالجة المشكلات العسكرية إبان الحرب. وسُمِّيَت مثل هذه الفرق بفرق بحوث العمليات. وقد نجح كلا الفريقين نجاحاً كبيراً في حل مشكلات عسكرية سواء كانت بحرية أم برية أم جوية.
بعد نهاية الحرب، بدأت القطاعات الاقتصادية بالاستفادة من هذه الأساليب في زيادة إنتاجها وربحها عن طريق الاستغلال الأفضل لمواردها. و يعد ظهور الحاسب وتطوره السريع عاملاً أساسياً في ازدهار بحوث العمليات و التوسع في استخدامها. كما يمكن القول إن أحد أهم العوامل التي ساعدت في تطور بحوث العمليات هو الرواج الاقتصادي الذي أعقب الحرب العالمية الثانية و ما صاحب ذلك من الاتساع في استخدام المكننة و الوسائل الآلية و تقسيم العمل و تفويض السلطات، الأمر الذي أدى إلى ظهور مشاكل إدارية كثيرة و معقدة مما دفع بعض العلماء و الباحثين إلى دراسة تلك المشكلات و إيجاد أفضل الحلول لها باستخدام أساليب بحوث العمليات.
يرجع السبب في تكوين فريق بحوث عمليات بدلاً من الاعتماد على الفرد الواحد إلى أن كثيراً من المشاكل الاستراتيجية و التكتيكية المرتبطة بالنواحي العسكرية معقدة جداً لدرجة أنه يتعذر على الفرد الواحد الوصول إلى حلول فرضية، و لذلك كان يتم تشكيل فريق لبحوث العمليات يتكون من عدد من العلماء ذوي تأهيل علمي متنوع، حتى يكون فريق بحوث العمليات قادراً على حل أية مشكلة تواجهه، ولكي يستطيع استخدام الوسائل العلمية الأفضل، فلا بد من أن يكون مكوناً من مختصين في الاقتصاد والرياضيات والإحصاء والإدارة والحاسب والعلوم الطبيعية وغيرها من العلوم حتى يلم هذا الفريق بجميع مجالات الحياة.
I – 3 مجال تطبيق علم بحوث العمليات
إن بحوث العمليات تستخدم الآن في مجالات عديدة، و لم تعد مقتصرة على النواحي العسكرية فقط، بل اتسع استخدامها ليشمل مجالات أخرى، ومنها:
1. المجال العسكري، وهنا يأتي دوره المهم في مجال الخطط الاستراتيجية واتخاذ القرارات والتوزيع الأمثل للإمكانات العسكرية المتاحة من عسكريين وأسلحة وطائرات ... الخ.
2. يستخدم في النواحي المالية، كالمصاريف وميزانية الدول وتوزيع الميزانية الأمثل في الأغراض المختلفة.
3. يستخدم في الصناعة، لذا تحتاج المصانع إلى هذا العلم لتقليل التكاليف وتحقيق أعظم ربح ضمن الإمكانات المتاحة.
4. في مجال الإنشاءات، لبناء الجسور والمشاريع الضخمة، لتقييم الوقت المستغرق لكل مشروع وتقليل هذا الوقت.
5. في الأسواق المالية والأسهم والتنبؤ عن الأوضاع الاقتصادية.
6. في إدارة المستشفيات وضبط عملية التغذية والأدوية ضمن الإمكانات.
7. في الزراعة والتسويق الزراعي.
وهناك مجالات أخرى لا حصر لها حتى تصل إلى بيتك لتنظيم المصروفات البيتية ضمن الإمكانات المتاحة.
I – 4 مراحل اتخاذ القرار
في ضوء التعاريف الواردة في بداية هذا الفصل نستطيع أن نذكر الآن تعريف بحوث العمليات كما صاغته جمعية بحوث العمليات البريطانية على وجه الخصوص لكونها الجمعية الأم لبحوث العمليات، و الجمعيات الأخرى تعد تفرعات و امتداداً لتلك الجمعية. إذ عرفت بحوث العمليات بأنها استخدام الأساليب العلمية لحل المشاكل المعقدة في إدارة أنظمة كبيرة من القوى العاملة و المعدات و المواد الأولية، والأموال في المصانع و المؤسسات الحكومية و في القوات المسلحة.
و أياً كان التعريف المعتمد في توضيح مفهوم بحوث العمليات فإنه يجب الإشارة إلى أن بحوث العمليات هي مجموعة البحوث والدراسات التي تساعدنا على اتخاذ قرار علمي ومدروس للقيام بعمل ما على أفضل وجه وضمن الإمكانات المتاحة. إن عملية اتخاذ القرار العلمي بحسب مفهوم بحوث العمليات و مهما كانت طبيعة هذه القرارات، تمر بعدد من المراحل التي لا بد من اتباعها إذا أردنا أن يكون القرار المتخذ سليماً. يمكن تمثيل مراحل اتخاذ القرار بالشكل (1). بناءً على هذا الرسم التوضيحي لخطوات اتخاذ قرار علمي ، يمكن تلخيص هذه الخطوات كما يأتي :
1. تحديد المشكلة أو الهدف ضمن افتراضات معينة تتناسب وطبيعة المشكلة أو مع رغبة متخذ القرار .
2. وضع نموذج فكري أو تصور لأبعاد المشكلة كلها . أي أن الدراسة هنا تعتمد على الخبرة والقدرة على التفكير العلمي المنظم الذي يسهل علينا إعداد النموذج المناسب لتحقيق الهدف الذي نريد .
3. إيجاد النموذج العلمي باستخدام الأساليب العلمية المناسبة.
يمكن أن نعد هذه الخطوات الثلاث مرحلة واحدة ، نسميها " النمذجة " .
الشكل (1): مراحل اتخاذ القرار
4. حل النموذج العلمي باستخدام الطرق الرياضية الموافقة ، والبحث عن أفضل الحلول وتطبيقها على المشكلة الحقيقية . وهذا يكون ممكناً باستخدام طرق البرمجة الرياضية .
سنعرض فيما يأتي معنى كلٍ من المصطلحين ، النمذجة و البرمجة الرياضية.
1 - 5 النمـذجـة ( Modeling )
النمذجة هي بالتعريف مجموعة إجراءات تتضمن عمليات معقدة مرتبطة ببعضها لإنشاء نموذج ممثل لمشكلة حقيقية . أي تمثيل المشكلة الحقيقية بشيء أبسط منها نسميه النموذج. ويمكن أن نصنف النماذج وفق ما يأتي :
1. نماذج فيزيائية : وهي تمثل أنظمة فيزيائية تكون تكلفة تصميمها كبيرة أو تأخذ وقتاً طويلاً . فيكون النموذج تبسيطاً لعرض هذا النظام الفيزيائي الحقيقي. و يكون الهدف من النمذجة هو تحليل سلوك النظام لمعرفة ميزاته (إذا كان النظام موجوداً ) أو من أجل إيجاد أفضل تصميم له في المستقبل (إذا كان النظام فكرة تنتظر التنفيذ ) .
2. نماذج ذهنية : يوجد هذا النوع من النماذج في عقل الإنسان فقط . ويتكون نتيجة لتراكم خبرات الإنسان وتجاربه . وهذه النماذج غالباً ما تكون غير واضحة وغير محددة ، ولا يمكن التعبير عنها بعلاقات من أي نوع ، ولكنها تساعد الإنسان على اتخاذ القرارات ورسم المخططات الضرورية لمسيرة حياته .
3. نماذج رمزية : و تتكون من نماذج رياضية وأخرى غير رياضية.
نقصد بالنمـاذج غير الرياضيـة ، نماذج لغويـة ( كلامية ) ، نماذج رسـوميـة و مخططات ... ، أما النماذج الرياضية فهي ولعدة أسباب تعد الأهم والأكثر استخداماً من سائر أنواع النماذج الأخرى .
I – 6 النمذجة الرياضية ( Mathematical Modeling )
هي التعبير عن الترابط بين المتغيرات الفيزيائية لنظام ما بعلاقات رياضية ، أو بشكل آخر .
النمذجة الرياضية هي صياغة مسألة ما وفق علاقات رياضية يطلق عليها اسم النموذج الرياضي .
ولتكوين نماذج رياضية لأي مسألة أو مشكلة مطروحة لا بد من اتباع الخطوات الآتية :
1. دراسة المشكلة المطروحة وتحديد غايتها ومكوناتها . فيجب أن تكون هناك غاية ما يراد الوصول إليها، مثل تأمين ربح أعظمي أو تأمين كلفة أصغرية أو تأمين توفير أعظمي بالوقت والجهد . كما يجب تحديد مجاهيل المسألة التي يجب إيجاد قيمها للوصول للغاية المطلوبة ، يمكن أن تكون هذه المجاهيل كميات إنتاج لمنتوجات معينة أو ساعات عمل في مؤسسة اقتصادية أو مبالغ من المال لفعاليات معينة أو كميات منقولة على طرق معينة وغير ذلك .
2. تحديد المدخلات والمخرجات في ضوء الإمكانات المتاحة ، وتحديد القيود المفروضة على المشكلة، فمثلاً الشركة لا تستطيع توفير أكثر من حجم معين من المواد الأولية لأسباب قد تكون خارجة عن إرادتها ، أو في نظام ميكانيكي مثلاً يجب ألا تزيد سرعته على حد معين .
3. بيان علاقات التأثير بين مجاهيل المسألة . فمثلاً في مصنع معين ، إذا زاد إنتاج أحد المنتوجات فإن ذلك سيؤدي إلى إنقاص الإنتاج من المنتوجات الأخرى . كما أن هناك شروطاً يجب أن تحققها هذه المجاهيل بغض النظر عن مردودها من حيث الغاية التي يجب تحقيقها . فمثلاً إذا كان أحد المجاهيل ممثلاً لكمية منتجة ، يشترط فيه ألا يكون سالباً ، وقد يفترض فيه ألا يقل عن أو أن يزيد على كمية معينة .
4. بعد تحديد كل ما ورد أعلاه فإنه بالإمكان صياغة المسألة ضمن علاقات رياضية بمجموعها نطلق عليها اسم " النموذج الرياضي " . وهذا النموذج هو تمثيل للمشكلة بصيغة رياضية قابلة للحل باستخدام إحدى الطرق أو الوسائل المتوافرة في بحوث العمليات .
ملاحظـة “ 1 “ :
بشكل عام لا تكون المسألة الحقيقية سهلة الترجمة إلى نماذج رياضية . حتى لو فرضنا أنه من الممكن ترجمة أي مسألة نصية إلى نموذج رياضي ، فإنه ليس من الضروري أن يكون لكل نموذج رياضي حلول . لذلك فإنه من الضروري أن نبسط المسألة أو نقربها إلى مسألة أخرى قريبة منها ، وفي الوقت نفسه تكون أسهل للترجمة إلى نموذج رياضي ، على أن نحافظ في أثناء عملية التقريب ( التبسيط ) لمسألة ما على كل الميزات الأساسية لها . فمثلاً ، عند دراسة حركة كوكب ، يمكن عده نقطة في الفضاء ونهمل حجمه وشكله .
ملاحظة “ 2 “ :
بعد إيجاد النموذج الرياضي وتفسير نتائجه وفق طبيعة المسألة الحقيقية ، فإننا نكون أمام إحدى حالتين:
• إذا كانت هذه النتائج جيدة ومُرْضية ، فإننا نكون قد وفقنا بإيجاد النموذج الرياضي الذي يمثل المسألة الحقيقية .
• وإذا لم تكن النتائج مُرْضية ، فإننا نحاول إجراء بعض التعديلات والتغييرات في الفرضيات التي اعتبرناها عند تقريب المسألة ، أو أن نبحث عن هيكل آخر للنموذج الرياضي .
| |
|
الأنيق...}
مستشار اداري


 عدد الرسائل : 216 عدد الرسائل : 216
العمر : 37
رقم العضوية : 700
تاريخ التسجيل : 26/10/2008
 |  موضوع: رد: بــحــوث الـعـمـلـيـات موضوع: رد: بــحــوث الـعـمـلـيـات  الأحد مارس 15, 2009 11:25 am الأحد مارس 15, 2009 11:25 am | |
| تابع بحوث العمليات البرمجة الخطية
Linear Programming
II – 1 مقدمة
رأينا في الفصل الأول من هذا الكتاب أنه يمكن اتخاذ أي قرار على مرحلتين رئيستين الأولى هي صياغة المسألة وفق علاقات رياضية يطلق عليها اسم النموذج الرياضي، و الثانية هي حل النموذج الرياضي و البحث عن أفضل الحلول و تطبيقها على المشكلة الحقيقية. و هذا يكون ممكناً باستخدام طرق البرمجة الرياضية. فماذا نعني بالبرمجة الرياضية؟
II - 2 البرمجة الرياضية Mathematical Programming
إن مسألة البرمجة الرياضية تعني – بشكل عام – البحث عن القيمة المثلى (صغرى أو عظمى ) لتابع جبري يضم عدة متغيرات . تخضع هذه المتغيرات لمجموعة من القيود تأخذ صيغة مساويات أو متراجحات .
• حيث X شعاع مركباته وهذه المركبات هي مجاهيل المسألة .
• التابع هو التابع الذي نرغب بإيجاد قيمته المثلى (عظمى أو صغرى) ويدعى تابع الهدف .
• مجموعة المتراجحات ، ومجموعة المساويات هي توابع معرفة في الفضاء وتدعى قيود المسألة .
• نسمي مجموعة الأشعة والتي تحقق جميع قيود المسألة بالحلول الممكنة . ونسمي المنطقة التي تحوي مجموعة الحلول الممكنة بمنطقة الإمكانيات.
• نسمي الشعاع الذي يحقق جميع قيود المسألة ويبلغ التابع فيه قيمته المثلى بالحل الأمثل .
إن حل مسألة البرمجة الرياضية يتطلب إذاً إيجاد الشعاع الذي يحقق جميع القيود ويُبْلِغ تابع الهدف قيمته المثلى .
ملاحظة “ 1 “ :
إن كلمة برمجة لم يكن لها علاقة بالحاسبات الإلكترونية في بادئ الأمر وإنما كانت تعني التخطيط . وهذا البرنامج الرياضي هو نموذج رياضي لمسألة ما II – 3 البرمجة الخطية Linear Programming
في مسألة البرمجة الرياضية ، إذا كان تابع الهدف ومجموعة القيود جميعها من الدرجة الأولى للمتحولات فإن البرنامج الرياضي يدعى برنامجاً خطياً . وتعد البرمجة الخطية من أوائل مواضيع بحوث العمليات. وقد بدأ بعرض مواضيعها العالم G-Stiegler بُعيد الحرب العالمية الثانية ، عندما حاول مقارنة الحد الأدنى لتكاليف المعيشة في ألمانيا قبل الحرب وبعدها ، فحصل على مسألة برمجة خطية .
إن تعبير البرمجة يعني وضع خطوات لحل مسألة ما لبلوغ هدف معين. أما تعبير خطية فيعني افتراض تغير الظاهرة التي نقوم بدراستها بصورة خطية (على شكل خط مستقيم) و كثيراً ما يستخدم هذا الافتراض لتقريب الواقع إلى صيغة رياضية سهلة.
تعد البرمجة الخطية احدى الوسائل المهمة في حل كثير من المشاكل الإدارية والاقتصادية و العسكرية، و قد ازداد تطبيقها في الآونة الأخيرة نظراً للتقدم التقني الذي ساعد على تطوير الحاسبات الالكترونية المستخدمة في حل مشاكل البرمجة.
II – 4 البرمجة غير الخطية Non-Linear Programming
إذا كان تابع الهدف أو أحد قيود مسألة برمجة رياضية من الدرجة الثانية فما فوق بالنسبة للمتحولات فإننا ندعوها مسألة برمجة غير خطية .
لقد عولجت مسائل البرمجة غير الخطية باستخدام طرق تقليدية قدمها رياضيو القرن السابع عشر والثامن عشر ( لاغرانج و نيوتن ، ... ) .
أما القفزة العظمى في هذا المجال ، فكانت عام 1951 عندما توصل كين– تيوكر ( Khun-Tuker ) إلى إضافة شروط جديدة على أسلوب مضاريب لاغرانج ، مما أدى إلى السيطرة على معظم مشاكل البرمجة غير الخطية .
II – 5 صياغة النماذج الرياضية
إن أهم مرحلة في البرمجة الخطية هي مرحلة إنشاء نموذج البرمجة الخطية، و نعني التعبير عن علاقات واقعية بعلاقات رياضية مفترضة و مبنية على دراسة الواقع وتحليله. من أجل صياغة نموذج البرمجة الخطية يجب توافر ثلاث مجموعات من العناصر الأساسية وهي:
• تحديد الهدف بصورة كمية. و يعبر عنه بتابع الهدف و هو عبارة عن التابع المطلوب إيجاد القيمة العظمى (أو الصغرى) له. يجب أن يكون بالإمكان التعبير عن الهدف كمياً كأن يكون الهدف تحقيق أكبر ما يمكن من الربح أو تأمين أصغر ما يمكن من الكلفة أو توفير أعظم ما يمكن من الوقت و الجهد.
• تحديد القيود. يحب أن تكون الموارد المتاحة محددة، كما يجب أن تكون تلك الموارد قابلة للقياس. و يتم التعبير عنها بصيغة رياضية على شكل متراجحات أو مساويات.
• تحديد البدائل المختلفة. و يشير هذا العنصر إلى أن يكون للمشكلة أكثر من حل واحد حتى يمكن تطبيق البرمجة الخطية. إذ لو كان للمشكلة حل واحد لما كانت هناك ضرورة لاستخدام البرمجة الخطية، إذ إن فائدتها تتركز في المساعدة على اختيار أفضل حل من بين الحلول المختلفة و المتعددة.
II – 6 أمثـلـة Examples
سنذكر فيما يأتي بعض الأمثلة البسيطة من مسائل اقتصادية تؤدي نمذجتها إلى برامج خطية .
مثـال “ 1 “ :
يقوم مصنع للألبسة بإنتاج أربعة أصناف من الملبوسات ( S4 , S3 , S2 , S1 ) ويستخدم من أجل ذلك المواد الأولية الآتية ( M3 , M2 , M1 ) . ترغب إدارة المصنع في دراسة التنظيم الأمثل للإنتاج خلال فترة زمنية ( شهر مثلاً ) وتحديد الإنتاج الشهري لكل منتوج من أجل تحقيق ربح أعظمي ، علماً بأن الربح يتناسب طرداً و عدد الوحدات المباعة من المنتوجات . نرتب المعلومات التي حصلنا عليها وفق الجدول الآتي :
المواد الأولية نـوع المنـتـج الكميات المتوافرة
S1 S2 S3 S4
M1 1.5 1 2.4 1 2000
M2 1 5 1 3.5 8000
M3 1.5 3 3.5 1 5000
ربح واحدة المنتج 5.24 7.3 8.34 4.18
نلاحظ أن هذا الجدول يوضح ما يأتي :1. الكميات المتوافرة من كل مادة أولية خلال الفترة الإنتاجية (شهر في مثالنا).
2. مقدار ما يلزم من كل مادة أولية في إنتاج واحدة منتج ( دستة مثلاً ) من كل من المنتوجات الأربعة.
3. الربح الناتج عن بيع واحدة المنتج من كل من المنتوجات الأربعة .
لنفرض أن x1 هو عدد الوحدات المنتجة من الصنف الأول S1 خلال الفترة الإنتاجية ( شهر في مثالنا ) . لنفرض أن x2 هو عدد الوحدات المنتجة من الصنف الثاني S2 خلال الفترة الإنتاجية ( شهر في مثالنا ). لنفرض أن x3 هو عدد الوحدات المنتجة من الصنف الثالث S3 خلال الفترة الإنتاجية ( شهر في مثالنا ). لنفرض أن x4 هو عدد الوحدات المنتجة من الصنف الرابع S4 خلال الفترة الإنتاجية ( شهر في مثالنا ).
إن الكميات المتوافرة من المواد الأولية هي مقادير محدودة ، و من ثم فإننا لا نستطيع زيادة الإنتاج بشكل عشوائي لأي منتج ، وإنما يجب توزيع الإنتاج بين الأصناف الأربعة بحيث يكون الربح أعظمياً و من غير تجاوز الكميات المتوفرة من كل مادة أولية من المواد الثلاث . كما أنه لا يمكن قصر الإنتاج على صنف واحد أو صنفين من الإنتاج فقط ، وذلك لضرورات السوق أو لتحقيق توازن في استهلاك المواد الأولية .
نلاحظ أنه يتم استهلاك كمية من المادة الأولية M1 في إنتاج الأصناف الأربعة من الملابس
اي انه يلزم كمية قدرها 1.5 من أجل إنتاج واحدة منتج من الصنف الأول ، علماً بأنه يتم إنتاج كمية قدرها x1 من الصنف الأول S1 . كما يلزم كمية قدرها 1 من أجل إنتاج واحدة منتج من الصنف الثاني ، علماً أنه يتم إنتاج كمية قدرها x2 من الصنف الثاني S2 . وهكذا بالنسبة لبقية الأصناف . ولكن مجموع ما يلزم من المادة الأولية M1 في إنتاج الأصناف الأربعة لا يمكن أن يتجاوز 2000 ( المقدار المتوافر من هذه المادة )
بالإضافة إلى ذلك ، فإنه لا يمكن إنتاج كميات سالبة ، فإما أن ننتج كمية موجبة من أي صنف أو ألا ننتج أي كمية على الإطلاق . وهو ما يسمى بشروط عدم السلبية .
بهذا نكون قد حددنا جميع القيود المفروضة على متحولات المسألة .
واضح أنه إذا تم إنتاج واحدات قدرها x4 , x3 , x2 , x1 من الأصنافS4 , S3 , S2 , S1 على الترتيب ، فإن الربح خلال الفترة الإنتاجية سوف يمثل تابع الهدف .
نرغب الآن في إيجاد قيم المنتوجات x4 , x3 , x2 , x1 التي تحقق القيود وتجعل الربح أعظم ما يمكن .
منقووووول | |
|
